代入の諸方法(2)

前節では、作用素が可換な場合の「代入算」 について述べたが、我々の扱う作用素は大抵可換ではない。 ここでは、非可換作用素の「代入算」の例として、 よく知られている フーリエ変換を用いた擬微分作用素の定義について 非可換幾何学的な考えを交えながら 述べてみよう。

前前節に少し述べたように、コタンジェントバンドル上の関数と 微分作用素とは「対応」している。

しかし、微分作用素だけを相手にするのでは、 コタンジェントバンドル上の関数の中でも、 ファイバー方向の変数について多項式であるようなもののみを 扱うことにあたり、(代数幾何の人以外の人にとっては) 嬉しくない。 コタンジェントバンドルは、美しい非可換幾何学的対象の影 であって、可換世界での事実は、量子世界の本物に対応物があるはず、 という立場に立てば、是非ともコタンジェントバンドル上の ( $C^{\infty}$ その他)いろいろなクラスに属する関数 に対応する「非可換関数環の元」を見つけ出したくなる。

言い方をかえれば、これはコタンジェントバンドル上の関数に微分 を代入することにあたる。このようにしてできた作用素は、 一般に擬微分作用素と呼ばれる。 (ただし、十分広い関数のクラスに代入することを考えると、 これは全ての作用素を考えることと同じになり、面白くないので、 関数のクラスを制限するのが普通である。 そうは言っても、 いろいろな作用素を微分作用素のような素性の良く分かった作用素で 表現している、 という点では便利であるので、クラスを広くとるのも全く無意味というわけではない。)

擬微分作用素の定義の仕方にもいろいろあるが、 良く知られているものの一つに、 (考えている多様体がユークリッド空間 $\mbox{${\Bbb R}$ }^n$ の場合に、) フーリエ変換 $\mathcal F$ とその逆変換 $\overline{\mathcal F}$ を巧妙に使う方法がある。 これは、フーリエ変換が x と id/dx との役割を入れ換えること、 および かけ算作用素(x の方) は簡単に関数に代入できる という事実を使ったもので、大まかに言って、

$$(f(x,id/dx)\phi)(x)=\overline{\mathcal F}_{\xi}[f(x,\xi)\mathcal F_{}[\phi](\xi))](x)$$

のように定義される。

この定義は「位置変数 x が前、運動量変数 p が後。」というならべかたの規則を 採用しているのとおなじである。 すなわち、f が x,p についての多項式の場合には、 (定数の係数を除いて、)

$$\sum_{i,j}x^i p^j \mapsto \sum_{i,j} x^i (d/dx)^j$$

のように対応させ、後はそれを適当な位相について連続に拡張している ことになる。

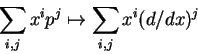
フーリエ変換を巧妙に用いたこのような方法はなかなか面白いものではあるが、 前述したようにこのような対応は「自然」なものではなく、 例えば考えている多様体を一般にした時には張り合わせの糊シロの部分で 少しつなぎ方を考えねばならなかったりする。 (したがって、実際には「コタンジェントバンドル上の関数に微分を代入する」 と言う言い方はすこしく正確性を欠いている。)

そのような事情のため、 T^*M を影として持つような非可換多様体上の関数環 (以下では仮に A と書くことにする。) として何を採用するかは、難しい問題になっている。

採用の基準として思い付くものをあげてみると、次のようになる。

• A には関数が少なすぎてはいけない。具体的には、 $C^{\infty}(M)$ の元、 および、自己共役な微分を前節の意味で $C^{\infty}$ 関数に代入した元は A に含まれるべきである。
• もっと一般に、A の自己共役な元を前節の意味で $C^{\infty}$ 関数に代入した元は A に含まれるべきである。
• A には関数が多すぎてはいけない。A は前二項を満たすような最小限の 環である。
• A は M に対して関手論的に定義される。
• $\mbox{${\Bbb R}$ }^n$ に対する A はフーリエ変換に関して不変である。

最初の三項でうまく定義できていると思う方がいるかも知れないが、 その定義では他の項目と矛盾してしまうようである。 「無限回微分できる」と言う素朴なアイディアを変更する必要が あるのではないか、とも思われる。

このような考察は、

熊ノ郷準著 擬微分作用素

の序文に書かれている「どのようなものを擬微分作用素と呼ぶか」 という問題と関連しているが、

たとえば e^d/dx (並行移動)のような元を考えに入れたいため、 A の元は一般には(上にあげた本で扱われているような) 擬局所性を持たないと覚悟すべき所が大きく違っている。

A の元は $\mbox{${\Bbb R}$ }^n$ のようなものを張り付ける接着材としての役割を担うため、 その解明は基本的であると考えられる。 今後の研究が待たれる所である。 (あるいは、既に知られているのなら是非筆者までお知らせください。)