


: with Fubini-Study 計量 を
: 複素射影空間
: 非可換環の「制限」
前節の「制限」の操作を シンプレクティック 多様体のほうでながめたのが、
シンプレクティック 商 である。
Lie 群 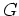 が シンプレクティック多様体
が シンプレクティック多様体
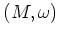 に作用し、
に作用し、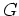 の
作用は
の
作用は 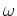 を不変にしているとする。
作用は次の様なリー環準同型を誘導する。
を不変にしているとする。
作用は次の様なリー環準同型を誘導する。
この作用の「モーメント写像」とは、この準同型の次のようなリフトのことである。
(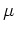 には「積分定数」の分だけ任意性があり、それをどう決めるかは場合による。
また、
には「積分定数」の分だけ任意性があり、それをどう決めるかは場合による。
また、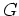 が不連結の場合には、
が不連結の場合には、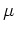 に適当な
に適当な 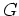 -共変性を要求する
必要がある。)
-共変性を要求する
必要がある。)
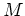 の
の 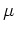 による「制限」がシンプレクティック 商 と
呼ばれるものである。
による「制限」がシンプレクティック 商 と
呼ばれるものである。
平成16年8月24日
![]() が シンプレクティック多様体
が シンプレクティック多様体
![]() に作用し、
に作用し、![]() の
作用は
の
作用は ![]() を不変にしているとする。
作用は次の様なリー環準同型を誘導する。
を不変にしているとする。
作用は次の様なリー環準同型を誘導する。
![]() の
の ![]() による「制限」がシンプレクティック 商 と
呼ばれるものである。
による「制限」がシンプレクティック 商 と
呼ばれるものである。