みんな大体気づいていると思うけど、式2で「どんな値でも」というのに
ちょっと嘘があるんだよね。実は、![]() は
は ![]() と似た意味で「不定」
と見倣すのが妥当だ。つまり、どっから見ても筋が通るように
一つの値に決めるのが不可能だ、ということなんだ。
と似た意味で「不定」
と見倣すのが妥当だ。つまり、どっから見ても筋が通るように
一つの値に決めるのが不可能だ、ということなんだ。
![]() は、
は、 ![]() の
の
![]() の時の極限と決められればいいんだけれど、
の時の極限と決められればいいんだけれど、
![]() を
を ![]() に近付ける方法はいろいろある。
に近付ける方法はいろいろある。
等々。なんだか ![]() の地点に
の地点に ![]() 二人の人が待ち合わせにいくみたいだ。
片方が遅れて来たり、一緒にいったり、片方がダッシュしてもう片方の
倍の速度で
二人の人が待ち合わせにいくみたいだ。
片方が遅れて来たり、一緒にいったり、片方がダッシュしてもう片方の
倍の速度で ![]() に近付いたり(きっとデートに遅刻しそうなんだな...)
に近付いたり(きっとデートに遅刻しそうなんだな...)
最後の例はちょっと難しいけれど、 ![]() が
が ![]() よりもむちゃくちゃに速く
よりもむちゃくちゃに速く
![]() に近付く例だ。
に近付く例だ。
前小節で既に言ったように、上のそれぞれの近付け方によって、
![]() がどの値に近付いていくかが変わってしまうんだ。
最後の2例については説明していなかったね。
がどの値に近付いていくかが変わってしまうんだ。
最後の2例については説明していなかったね。
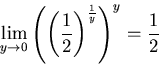
これを読んでいる皆さんもぜひ ![]() をいろんな値に近付けてみて欲しい。
簡単で気の効いているやり方が分かったら
私([email protected])宛に送りつけると私はとっても喜ぶだろう。
をいろんな値に近付けてみて欲しい。
簡単で気の効いているやり方が分かったら
私([email protected])宛に送りつけると私はとっても喜ぶだろう。
とにかく、![]() は
は
![]() の近付き方によって
の近付き方によって ![]() から
から ![]() までの
どんな実数値にもなり得る。
(このことは
までの
どんな実数値にもなり得る。
(このことは
![]() のグラフを見てみるともっと良くわかるね。
のグラフを見てみるともっと良くわかるね。
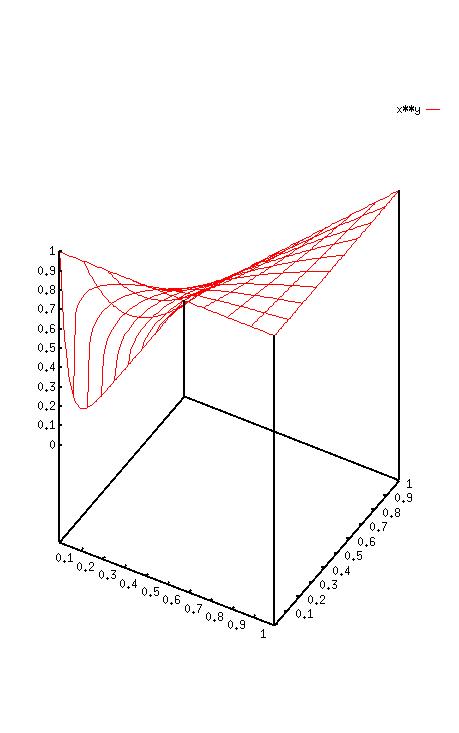
上図で、![]() のグラフは、x,y が 0に近付くと
のグラフは、x,y が 0に近付くと ![]() 軸にヘバリついてくるのが
見てとれるかな?)
軸にヘバリついてくるのが
見てとれるかな?)
だから ![]() は不定だ、と呼ばれるんだね。
は不定だ、と呼ばれるんだね。