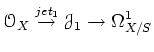The sheaf of differential 1-forms as the universal derivation

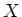Let $X$ be a separated 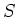$S$ -scheme. We define derivative

$$d: \mathcal{O}_X \to \Omega_{X/S}^1$$

as follows

$$\mathcal{O}_X \overset{jet_1}{\to} \mathcal J_{1} \to \Omega_{X/S}^1$$

PROPOSITION 9.19   For any sheaf homomorphism $\varphi: \Omega^1_{X/S},\mathcal{F})$ ,

$$f\mapsto \varphi(df)$$

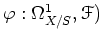is a derivation from 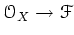$\mathcal{O}_X \to \mathcal{F}$ relative to 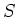$S$ . This assignment yields a isomorphism of 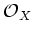$\mathcal{O}_X$ -module

$$\mathscr{D}er_{X/S}(\mathcal{O}_X,\mathcal{F}) \cong \mathscr{H}om(\Omega^1_{X/S},\mathcal{F}).$$