curvature revisited

In this subsection we prove an important proposition on curvature. But before we do that, we do two things. Firstly, we prove the following lemma.

LEMMA 5.7   Let $A$ be a commutative ring. Let $B$ be a commutative $A$ -algebra. Then for any $X,Y\in \operatorname{Der}_A(B)$ and for any $\omega\in \Omega^1_{X/S}$ , we have

$$i_Y i_X (d \omega) = X. \langle \omega,Y\rangle - Y.\langle \omega,X \rangle -i_{[X,Y]}\omega .$$

PROOF..

$$i_Y i_X d \omega$$

$$= i_Y (L_X-d i_X)\omega$$

$$= i_Y (L_X \omega)-i_Y d \langle \omega,X \rangle$$

$$= L_X (i_Y \omega)-i_{[X,Y]}\omega - Y.\langle \omega,X \rangle$$

$$= X. \langle \omega,Y\rangle -i_{[X,Y]}\omega - Y.\langle \omega,X \rangle$$

$\qedsymbol$

Secondly, we add a notation.

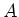
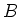
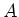
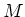
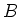
DEFINITION 5.8   Let $A$ be a commutative ring. Let $B$ be a commutative $A$ -algebra. Let $M$ be a $B$ -module with a connection

$$\nabla: M\to \Omega^1_{B/A}\otimes_B M.$$

Then for any $X\in \operatorname{Der}_A(B)$ ,

$$(i_X\otimes 1)\nabla : M \to M$$

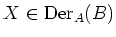
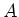
is an $A$ -linear map. We shall denote it by $\nabla_X$ .

PROPOSITION 5.9   Let $A$ be a commutative ring. Let $B$ be a commutative $A$ -algebra. Let $M$ be a $B$ -module with a connection

$$\nabla: M\to \Omega^1_{B/A}\otimes_B M.$$

Let $R$ be the connection $2$ -form of $\nabla$ . Then for any $X,Y\in \operatorname{Der}_A(B)$ , we have

$$\langle R, X \wedge Y\rangle_\wedge =[\nabla_X,\nabla_Y]-\nabla_{[X,Y]}$$

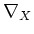
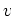
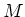
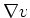
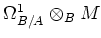
PROOF.. Let $v$ be an element of $M$ . Since $\nabla v$ is an element of $\Omega^1_{B/A}\otimes_B M$ , we may write it as :

$$\nabla v=\sum_j \omega_j \otimes v_j$$

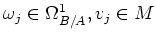
for some $\omega_j \in \Omega^1_{B/A}, v_j \in M$ . Then we compute

$$\nabla \nabla v =\sum_j d \omega_j \otimes v_j - \sum_j \omega_j \wedge \nabla v_j.$$

$$i_Y i_X \nabla \nabla v$$

$$= ((i_Y i_X )(d \omega_j)) \otimes v_j -i_Y \sum_j \langle \omega_j,X\rangle \nabla v_j +\sum_j \omega_j \nabla_X v_j$$

$$= (i_Y i_X d \omega_j)\otimes v_j -\sum_j \langle \omega_j , X) \nabla_Y v_j +\sum_j \langle \omega_j , Y) \nabla_X v_j$$

On the other hand, we have

$$\nabla_X(v) =(i_X\otimes 1)\nabla(v))=\sum_j \langle \omega_j,X\rangle v_j$$

So we may proceed

$$\nabla \nabla_X(v) =\sum_j d \langle \omega_j,X\rangle v_j +\sum_j \langle \omega_j,X\rangle \nabla v_j$$

$$\nabla_Y \nabla_X(v) =\sum_j Y. \langle \omega_j,X\rangle v_j +\sum_j \langle \omega_j,X\rangle \nabla_Y v_j$$

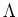
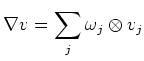
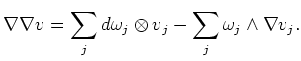
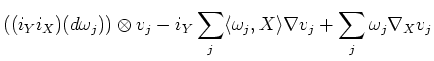
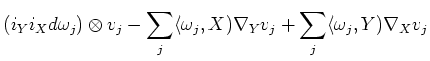
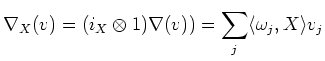
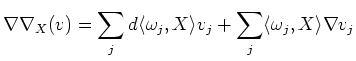
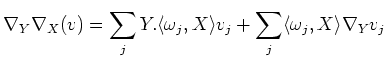
Thus, together with the Lemma above, we see

$$i_Y i_X \nabla \nabla (v)+ \nabla_Y \nabla_X(v)-\nabla_X\nabla_Y(v) =-\sum_j i_{[X,Y]}\omega_j \otimes v_j=-\nabla_{[X,Y]} v$$

$\qedsymbol$

COROLLARY 5.10   If the curvature $R$ of $\nabla$ is equal to zero, then

$$\nabla_{\bullet}: \operatorname{Der}_A \to \operatorname{End}_A(M)$$

is a Lie algebra homomorphism.