ïŋ―ïŋ―12ïŋ―ïŋ―ïŋ―ÜĪΞïŋ―ïŋ―ïŋ― :
![]()
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
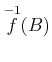 ïŋ―ïŋ―
ïŋ―ïŋ―
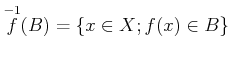
ïŋ―ËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
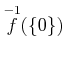 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
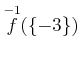 ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
![$ \overset{-1}{f}([1,5])$](img17.png) ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―čĄĢ
![$ \overset{-1}{f}([3,4])$](img18.png) ïŋ―ïŋ―ïŋ―ČĪïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ČĪïŋ―čĄĢ
ïŋ―ïŋ―ïŋ―ĖĪËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―
ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĄïŋ―![]() ïŋ―Îļïŋ―ïŋ―ïŋ―
ïŋ―Îļïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ÍĪËĪïŋ―ÃĪïŋ―
ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ÍĪËĪïŋ―ÃĪïŋ―
ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
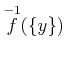 ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ―
ïŋ―ÎĪïŋ―ïŋ―ČĪïŋ― 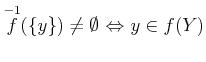 .
.
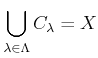 .
.
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ÍīØ·ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ÏĄïŋ―ïŋ―ÖĨïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―É―ïŋ―ïŋ―ņĪŊĄŨĪïŋ―ïŋ―ČĪËĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪčĪĶïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĄïŋ―ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ïŋ―ËĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ïŋ―
ïŋ―ïŋ―
![]() ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđïŋ―ĮĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪßĪïŋ―Č―ïŋ―ęĪđïŋ―ïŋ―ÞĨïŋ―ïŋ―ïŋ―ŨĪïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđïŋ―ĮĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđïŋ―ĮĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ÎĪßĪïŋ―Č―ïŋ―ęĪđïŋ―ïŋ―ÞĨïŋ―ïŋ―ïŋ―ŨĪïŋ―Íŋïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÆĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÉĪïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―Æąïŋ―ÍīØ·ïŋ―ïŋ―ŨĪČĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―Įļïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ÎĄïŋ―Æąïŋ―ÍĄŨĪČĪïŋ― (ïŋ―ïŋ―ïŋ―Îŋïŋ―ïŋ―ĖĪïŋ―ïŋ―éĪĪïŋ―ËĪÏĪïŋ―ïŋ―ïŋ―ïŋ―ëĪŽ)ïŋ―ïŋ―ïŋ―ïŋ―ĘŠïŋ―ĮĪïŋ―ïŋ―ëĄĢïŋ―čĪŊïŋ―ïŋ―ïŋ―ĖĪïŋ―ïŋ―ëĪģïŋ―ČĄïŋ―
ïŋ―ïŋ―ïŋ―ÝĪïŋ―ïŋ―ïŋ―Č―ïŋ―ęĪđïŋ―ïŋ―ÐĄïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ïŋ―ČĪōžĻĪïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
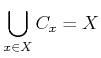 .
.
ïŋ―ïŋ―ÛĪÉĪïŋ―Æąïŋ―ÍĪËĄïŋ―![]() ïŋ―ÎĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ęĄĒ
ïŋ―ÎĪĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĘĢïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÎĪïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ČĪËĪïŋ―ęĄĒ
![]() ïŋ―ÎĨïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―Æ°ŨĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―ïŋ―åĩ2ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏļßĪïŋ―ïŋ―ËĩÕĪËĪĘĪÃĪÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪČĪïŋ―Æąïŋ―ÍīØ·ïŋ―ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―Üžïŋ―ÅŠïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÎĨïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―Æ°ŨĪïŋ―ĘŽïŋ―ïŋ―ïŋ―ïŋ―čĪĶïŋ―ËĄïŋ―ïŋ―åĩ2ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÏļßĪïŋ―ïŋ―ËĩÕĪËĪĘĪÃĪÆĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ĘĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪČĪïŋ―Æąïŋ―ÍīØ·ïŋ―ïŋ―ïŋ―Íŋïŋ―ïŋ―ïŋ―ëĪģïŋ―ČĪïŋ―
ïŋ―Üžïŋ―ÅŠïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―
ïŋ―ÖĨÛĨÆĨïŋ―ŌĨïŋ―ŲĨïŋ―ČĄïŋ―ÅŠïŋ―ïŋ―É―ïŋ―ïŋ―ïŋ―ōĪ·ĪÆĪßĪčĪĶïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ËĪïŋ―ęĄĒ
ïŋ―ËĪïŋ―ęĄĒ![]() ïŋ―ÎĪïŋ―ïŋ―ėĪūïŋ―ïŋ―ïŋ―
ïŋ―ŌĨČĪÏĨÛĨÆĨïŋ―
ïŋ―ÎĪïŋ―ïŋ―ėĪūïŋ―ïŋ―ïŋ―
ïŋ―ŌĨČĪÏĨÛĨÆĨïŋ― ![]() ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ÎĪïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ëĄĢ
![]() ïŋ―ČĪÏĄïŋ―
ïŋ―ČĪÏĄïŋ―
![]() ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ― ![]() ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĪģïŋ―ČĪïŋ―ïŋ―ĖĢïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ÃĪïŋ―
ïŋ―ïŋ―ïŋ―ïŋ―Æąïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÞĪëĪģïŋ―ČĪïŋ―ïŋ―ĖĢïŋ―ïŋ―ïŋ―ëĄĢ
ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ËĪïŋ―ÃĪïŋ― ![]() ïŋ―ÎĨïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÔĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïĪąïŋ―ĮĪïŋ―ïŋ―ëĄĢ
ïŋ―ÎĨïŋ―ïŋ―éĨđĘŽïŋ―ïŋ―ïŋ―ïŋ―ïŋ―ÔĪïŋ―ïŋ―ïŋ―ČĪïŋ―ïŋ―ïŋ―ïŋ―ïĪąïŋ―ĮĪïŋ―ïŋ―ëĄĢ