微分積分学基礎 No.1要約
今日のテーマ:実数
関数の概念:
定義 1.1
集合
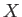
上の実数値関数
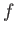
とは、
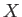
の各元
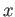
に対して、その値
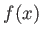
が
(誰がやっても正しくやる限りはただひとつ)定まっている時に
いう。
「ある時刻での気圧」は平面の領域上の関数とみなせる。
→多変数関数や関数列を扱う必要が生じる。
ただし、まずは
数列や、一変数関数を扱うのが基本になる。
定義 1.2
以下この講義では次のような記号を用いる。
-
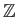 : 整数全体のなす集合。
: 整数全体のなす集合。
-
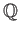 : 有理数全体のなす集合。
: 有理数全体のなす集合。
-
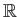 : 実数全体のなす集合。
: 実数全体のなす集合。
-
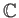 : 複素数全体のなす集合。
: 複素数全体のなす集合。
定義 1.4
実数
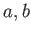
について、閉区間
![$ [a,b]$](img14.png)
と開区間
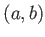
を
つぎの式で定める。
以下、この講義では、
整数、有理数、実数の、和、差、積、商、等号、不等号。を
自由に用いる。
その他、実数の完備性というのも用いるのであるが、それについては次回以降。
数列
定義 1.5
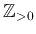
上の関数を数列という。数列のことを
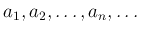
と書いたり、
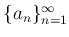
と書いたりする。
単に数列と言ったときには、有限数列は考えない。
他方で、「(添字が)0 から始まる数列」なども場合によっては考えることがあるが、
それについては臨機応変に。
◎有界
定義 1.6
-
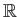 の部分集合
の部分集合 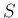 が有界であるとは、
ある実数
が有界であるとは、
ある実数 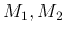 があって、どのような
があって、どのような 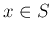 に対しても
に対しても
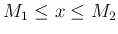 を満たすときに言う。
を満たすときに言う。
- 実数列
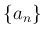 が有界であるとは、
それを
が有界であるとは、
それを
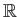 の部分集合と見て有界であるときに言う。
の部分集合と見て有界であるときに言う。
- 集合
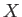 上の関数
上の関数 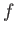 が有界であるとは、値集合
が有界であるとは、値集合
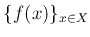 が有界であるときにいう。
が有界であるときにいう。
(2) は (3)の特別の場合とも見ることができる。(3)については次回以降に解説する。
◎極限
定義 1.7
数列
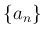
は、ある実数
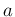
にたいして、
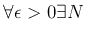
such that
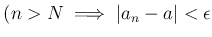
をみたすとき、
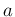
に
収束する という。
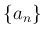
が
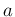
に収束するとき、 その収束する先
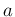
は一つに定まる。そこで
この値のことを
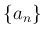
の
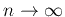
のときの
極限とよび、
と表す。
命題 1.8
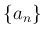
と
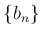
とが収束すると仮定する。このとき、
- さらに
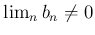 を仮定すると、
有限個の例外を除いて
を仮定すると、
有限個の例外を除いて 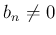 で、
で、