微分積分学基礎 No.2要約
今日のテーマ:(実数区間上の)連続関数
定義 2.1
実数
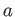
を含む区間上で定義された関数
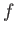
にたいして、
実数
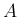
が、
を満たすとき、
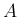
は
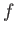
の
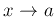
での極限であるといい、
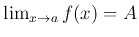
と表記する。
定理 2.2
極限は存在するとすれば一つである。
極限は和、差、積、(分母が0でない)商をたもつ。
定義 2.3
実数
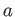
を含む区間
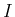
上で定義された関数
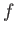
が、
を満たすとき、
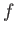
は
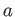
で連続であるという。
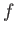
が
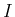
の全ての点で連続であるとき、
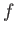
は
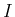
で連続であるという。
命題 2.4
区間
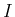
を固定すると、
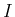
上の 連続関数
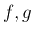
の和、差、積は連続である。I
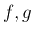
が連続で、
上の各点
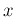
で
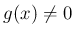
なら、
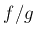
も
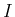
上で連続である。