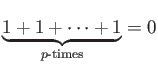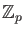 ,
,
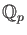 , and the ring of Witt vectors
, and the ring of Witt vectors
Yoshifumi Tsuchimoto

You should know that every positive integer may be written in
decimal notation:
Similarly, given any integer (“base”) 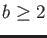 ,
we may write a number as a string of digits in base
,
we may write a number as a string of digits in base 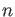 .
For example, we have
.
For example, we have
Similarly, we have
You may also probably know (repeating) decimal expresions
of positive rational numbers.
Now let us reverse the order of digits.
Namely, we employ a notation like this1:
Let us do some calculation with the above notation:
You may recognize curious rules of computations.
This curious notation will lead you to a new world called “the world of
addic numbers”.
EXERCISE 0.1
Compute
with our curious notation.
Then do the same computation in the usual digital notation in base
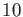
.
LEMMA 0.1
For any prime number 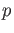 ,
,
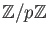 is a field.
(We denote it by
is a field.
(We denote it by
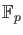 .)
.)
LEMMA 0.2
Let 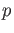 be a prime number.
Let
be a prime number.
Let 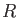 be a commutative ring which contains
be a commutative ring which contains
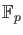 as a subring.
Then we have the following facts.
as a subring.
Then we have the following facts.
holds in 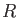 .
.
- For any
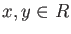 , we have
, we have
We would like to show existence of “finite fields”.
A first thing to do is to know their basic properties.
The next task is to construct such fields. An important tool is
the following lemma.
LEMMA 0.4
For any field 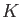 and for any non zero polynomial
and for any non zero polynomial ![$ f\in K[X]$](img35.png) ,
there exists a field
,
there exists a field 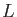 containing
containing 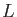 such that
such that
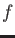 is decomposed into linear factors in
is decomposed into linear factors in 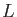 .
.
To prove it we use the following lemma.
Then we have the following lemma.
Finally we have the following lemma.
LEMMA 0.7
Let 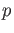 be a prime number. Let
be a prime number. Let 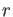 be a positive integer.
Let
be a positive integer.
Let 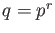 . Then we have the following facts.
. Then we have the following facts.
- There exists a field which has exactly
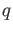 elements.
elements.
- There exists an irreducible polynomial
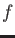 of degree
of degree 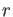 over
over
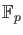 .
.
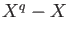 is divisible by the polynomial
is divisible by the polynomial 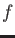 as above.
as above.
- For any field
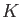 which has exactly
which has exactly 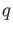 -elements, there exists an element
-elements, there exists an element
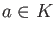 such that
such that 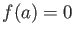 .
.
In conclusion, we obtain:
THEOREM 0.8
For any power 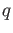 of
of 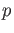 , there exists a field which has exactly
, there exists a field which has exactly 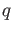 elements.
It is unique up to an isomorphism. (We denote it by
elements.
It is unique up to an isomorphism. (We denote it by
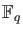 .)
.)
![]()