Next: About this document ... Up: , , and the Previous: The ring of -adic
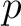 -adic Witt vectors for general
-adic Witt vectors for general 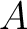
 of universal Witt vectors decomposes into a countable direct sum of
the ring of
of universal Witt vectors decomposes into a countable direct sum of
the ring of 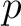 -adic Witt vectors. In this subsection we show that
the ring
-adic Witt vectors. In this subsection we show that
the ring
 can be defined for any ring
can be defined for any ring 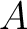 (that means, without
the assumption of
(that means, without
the assumption of 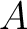 being characteristic
being characteristic 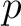 ).
).
We need some tools.
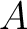 be any commutative ring.
Let
be any commutative ring.
Let  be a positive integer. Let us define additive operators
be a positive integer. Let us define additive operators  on
on
 by the following formula.
by the following formula.


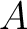 is an algebra over
is an algebra over
 . Then the definition descends to
a formal law defined over
. Then the definition descends to
a formal law defined over
 so that
so that  is defined for any ring
is defined for any ring 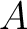 .
In other words,
.
In other words,  is
actually defined to be the unique continuous additive map which
satisfies
is
actually defined to be the unique continuous additive map which
satisfies

 be a prime number.
Let
be a prime number.
Let 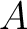 be a commutative ring of characteristic
be a commutative ring of characteristic  .
Then:
.
Then:

 is an algebra endomorphism of
is an algebra endomorphism of
 in this case.
in this case.

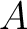 be any commutative ring.
Let
be any commutative ring.
Let 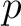 be a prime number.
We denote by
be a prime number.
We denote by



![$\alpha_j(X,Y)\in \mathbb{Z}[X,Y]$](img110.png) by the following relation.
by the following relation.


 and
and  on
on
 such that the following diagrams commute.
such that the following diagrams commute.


 .
It is easier to see that the multiplication also descends.
.
It is easier to see that the multiplication also descends.

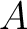 ,
elements of
,
elements of
 are called
are called 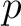 -adic Witt vectors over
-adic Witt vectors over 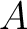 .
The ring
.
The ring
 is called
the ring of
is called
the ring of 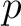 -adic Witt vectors over
-adic Witt vectors over 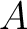 .
.
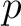 be a prime number.
Let
be a prime number.
Let 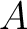 be a ring of characteristic
be a ring of characteristic 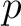 .
Then for any
.
Then for any  which is not divisible by
which is not divisible by 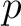 , the map
, the map

 . That means,
. That means,

 is already shown to be additive. The following calculation
shows that
is already shown to be additive. The following calculation
shows that
 preserves the multiplication:
for any positive integer
preserves the multiplication:
for any positive integer  with lcm
with lcm  and for any element
and for any element  ,
we have:
,
we have:
 | ||
 |
 | |
 |
 | |
 |
 |
![$[1]$](img26.png) of the
Witt algebra is equal to
of the
Witt algebra is equal to
![$\frac{1}{n}V_n ([1] )= e_n$](img130.png) and that
and that
 for any
for any
 .
The rest is then obvious.
.
The rest is then obvious.

In preparing from No.7 to No.10 of this lecture, the following reference (especially its appendix) has been useful:
http://www.math.upenn.edu/~chai/course_notes/cartier_12_2004.pdf