


: Q3.さらに、このWは非可測な集合になるのでしょうか?
: 疑似指数 Q and A
: Q1 実数全体のなす空間 が 上のベクトル空間になることは分かりますが、
A2.
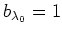 を含むような基底をとってください。
2
を含むような基底をとってください。
2
A1 と同様の手法により、
このような基底が存在することが分かります。
とおくと、
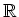
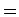
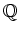
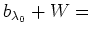
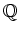
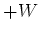 が成り立ちます。
が成り立ちます。
さて、任意の実数 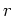 にたいして、
にたいして、
と一意的に書けます。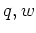 は
は 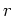 に関して
に関して
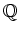 -線型です。
-線型です。
そこで、疑似指数関数 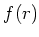 をたとえば
をたとえば
などで定義すれば、
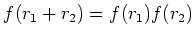 が成り立つことが確かめられます。
が成り立つことが確かめられます。
2002年10月9日
![]() を含むような基底をとってください。
2
を含むような基底をとってください。
2
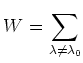
![]() にたいして、
にたいして、
![]() をたとえば
をたとえば