: 三角関数の定義余話
: 単行本サポートページ
: 単行本サポートページ
0 の 0 乗は不定、これにて一件落着、でもよさそうなものだけれども、
例えば多項式
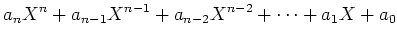 |
(A) |
のことを
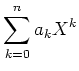 |
(B) |
と書いたときに、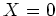 を代入すると、定数項の部分に
を代入すると、定数項の部分に 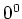 が
現れるのを気になさる方も
あるようです。このような場合には、(B)は (A)の略記に過ぎず、(B) に形式的に
現れる
が
現れるのを気になさる方も
あるようです。このような場合には、(B)は (A)の略記に過ぎず、(B) に形式的に
現れる 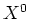 というのは実は
というのは実は 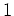 であると約束している
というのが正しい説明でしょう。
講義や、本などではついついそのような説明は
往々にして省かれてしまっています。
ベキ級数の扱いでも同じことが言えます。
(
であると約束している
というのが正しい説明でしょう。
講義や、本などではついついそのような説明は
往々にして省かれてしまっています。
ベキ級数の扱いでも同じことが言えます。
(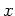 の
の 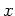 乗の話でもそうですね。反省。反省。)
乗の話でもそうですね。反省。反省。)
コダワリ派には注意が必要かも知れません。
(注意のしすぎにも注意。)
平成16年11月14日