


: 環 の表現と -加群との対応
: -表現以外の環 の表現
: が正の整数の時
前小節の最後で、
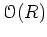 と
と 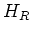 との関係が出て来た。
との関係が出て来た。
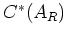 は
は
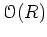 上の微分作用素のなす層
上の微分作用素のなす層
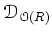 のグローバルセクションと見倣すこともできる。
(ただし、
のグローバルセクションと見倣すこともできる。
(ただし、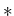 -構造は今しばらく忘れておく必要がある。)
もちろん、
-構造は今しばらく忘れておく必要がある。)
もちろん、
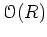 がラインバンドルとして意味をなすためには
がラインバンドルとして意味をなすためには
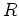 は整数でなければならない。しかし
は整数でなければならない。しかし
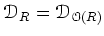 を
(
を
(
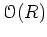 への作用を忘れて)単なる環の層として眺めてみると、
実はこれは
への作用を忘れて)単なる環の層として眺めてみると、
実はこれは 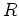 が任意の実数でも定義をすることができることが知られている。
([1] [2])
一般の実数
が任意の実数でも定義をすることができることが知られている。
([1] [2])
一般の実数 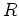 に対して、「
に対して、「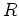 -次斉次なregularな関数」は存在しないのだが、
-次斉次なregularな関数」は存在しないのだが、
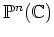 上で analytic topology について local には
上で analytic topology について local には
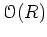 の元にあたるものが存在する。
それに対する微分作用素を
の元にあたるものが存在する。
それに対する微分作用素を
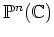 に
おろして来たのが
に
おろして来たのが
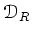 だと見ることができる。
だと見ることができる。
このことを考えると、
《 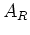 は
は
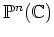 上のグローバルなオブジェクトとして
は捉えられないが、
上のグローバルなオブジェクトとして
は捉えられないが、
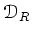 がその類似物を提供している》
と見ることもできる。次の小節でこの点について少し補足することにしておこう。
がその類似物を提供している》
と見ることもできる。次の小節でこの点について少し補足することにしておこう。
(ただし 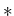 に関する対称性から見れば
この見方が完全に満足のいく見方とは言いがたい。
むしろ、
に関する対称性から見れば
この見方が完全に満足のいく見方とは言いがたい。
むしろ、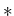 に対する
に対する 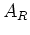 の対称性は、
の対称性は、
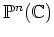 上の特定の加群の層に対して、
双対性(Fourier変換にあたる) を定義していると見ることもできる。)
上の特定の加群の層に対して、
双対性(Fourier変換にあたる) を定義していると見ることもできる。)
平成16年8月24日
![]() は
は
![]() 上のグローバルなオブジェクトとして
は捉えられないが、
上のグローバルなオブジェクトとして
は捉えられないが、
![]() がその類似物を提供している》
と見ることもできる。次の小節でこの点について少し補足することにしておこう。
がその類似物を提供している》
と見ることもできる。次の小節でこの点について少し補足することにしておこう。
![]() に関する対称性から見れば
この見方が完全に満足のいく見方とは言いがたい。
むしろ、
に関する対称性から見れば
この見方が完全に満足のいく見方とは言いがたい。
むしろ、![]() に対する
に対する ![]() の対称性は、
の対称性は、
![]() 上の特定の加群の層に対して、
双対性(Fourier変換にあたる) を定義していると見ることもできる。)
上の特定の加群の層に対して、
双対性(Fourier変換にあたる) を定義していると見ることもできる。)